Quick Analysis of Armenia CEC Data #armvote13

Raffi Hovhannisyan and his supporters have rallied in Yerevan, claiming that he is the duly elected president. OSCE observers issued a report that both praised and challenged the process, noting that observers found evidence of "[u]ndue interference in the process, mainly by proxies representing the incumbent, and some cases of serious violations, including intimidation of voters...in a number of polling stations."

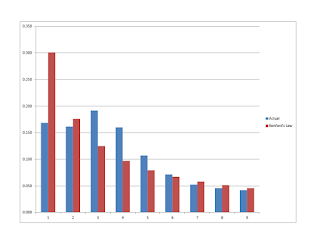
The data suggest that some anomalies are present. Using the CEC data for polling stations, I assessed the first and second digit distributions based on expectations from Benford's Law. This approach, in principle, can reveal anomalies in data that may be due to some form of manipulation. But, it is critical to note that scholars who evaluate data in this manner (such as forensic accountants) have cautioned about the over-interpretation of a single test.

The figure and tables below show the results of first- and second-digit evaluations on 1,988 polling station results for Serzh Sargsyan. Apologies for the ocular "tests," but some of the functions on my macros are not working at the moment. Second digits largely conform with expectations, but first-digit distributions suggest that anomalies may have been present. Note, for example, that the distribution of 1s is substantially lower than expected while 3s, 4s, and 5s are higher. 

Table 1: Serzh Sargsyan

1st Digit	Count	Actual	Benford's Law	Diff	Signif
1	335	0.169	0.301	-0.133	12.857
2	321	0.161	0.176	-0.015	1.682
3	381	0.192	0.125	0.067	8.962
4	318	0.160	0.097	0.063	9.465
5	213	0.107	0.079	0.028	4.576
6	142	0.071	0.067	0.004	0.755
7	104	0.052	0.058	-0.006	1.035
8	91	0.046	0.051	-0.005	1.037
9	83	0.042	0.046	-0.004	0.801
2nd Digit		Actual	Benford's Law
0	243	0.122	0.120	0.003	0.316
1	240	0.121	0.114	0.007	0.924
2	218	0.110	0.109	0.001	0.084
3	195	0.098	0.104	-0.006	0.874
4	194	0.098	0.100	-0.003	0.367
5	187	0.094	0.097	-0.003	0.357
6	177	0.089	0.093	-0.004	0.626
7	181	0.091	0.090	0.001	0.069
8	181	0.091	0.088	0.003	0.509
9	172	0.087	0.085	0.002	0.203

The Hovhannisyan data also evidence some anomalies, notably lower than expected 1s, 6s, 7s, 8s, and 9s, and higher than expected 3s, 4s, and 5s in the first digits.

Table 2: Raffi Hovhannisyan

1st Digit	Count	Actual	Benford's Law	Diff	Signif
1	331	0.177	0.301	-0.124	11.619
2	332	0.178	0.176	0.002	0.177
3	404	0.217	0.125	0.092	11.928
4	392	0.210	0.097	0.113	16.485
5	211	0.113	0.079	0.034	5.380
6	95	0.051	0.067	-0.016	2.725
7	40	0.021	0.058	-0.037	6.707
8	32	0.017	0.051	-0.034	6.615
9	29	0.016	0.046	-0.030	6.191
2nd Digit		Actual	Benford's Law
0	218	0.117	0.120	-0.003	0.344
1	214	0.115	0.114	0.001	0.072
2	205	0.110	0.109	0.001	0.107
3	175	0.094	0.104	-0.011	1.452
4	172	0.092	0.100	-0.008	1.131
5	187	0.100	0.097	0.004	0.477
6	190	0.102	0.093	0.008	1.215
7	177	0.095	0.090	0.005	0.638
8	163	0.087	0.088	0.000	0.033
9	165	0.088	0.085	0.003	0.489

Ballot invalidation and turnout data provide interesting information as well. No ballots were invalidated in 125 polling stations, and in 57 polling stations the invalidation rates were above 10%.* Low levels of invalidation (especially cases where no ballots are invalidated) are unusual and could be consistent with ballot box stuffing, alteration of protocols or other actions. High levels of invalidation, especially with a simple ballot like the one Armenian voters encountered, may also be consistent with manipulation.

The figure below plots the proportion of vote received (y axis) by turnout (x axis) using polling station data. At higher levels of turnout,** Sargsyan's performance (in red) is better relative to Hovhannisyan (in blue). This type of outcome has been interpreted in other countries as suggestive of manipulation.

What the data tell us:

• Based on first-digit tests, polling station results reveal anomalies in the distribution of data.
• Around 6% of polling stations reported no invalid ballots. Except in small (or special) polling stations, it is unusual for voters to make no errors on their ballots.
• Higher levels of turnout produced, in general, better outcomes for the incumbent president.

While the data suggest that more scrutiny of the electoral process is warranted, they do not "prove" that fraud occurred. A deeper assessment is necessary to rule out alternate explanations (e.g., better mobilization for Sargsyan in certain regions, etc.). In addition, even if fraud occurred, the data we have at the moment cannot "prove" that the outcome would have been different if no manipulation were present. 

* These higher levels of invalidation were not only located in polling stations with few registered voters.
** Calculated using columns 10 ("total number of electors") and 11 ("the number of participants of voting") in the CEC data.